中央値について 真ん中の落とし穴に気をつけろ 苦手な数学を簡単に
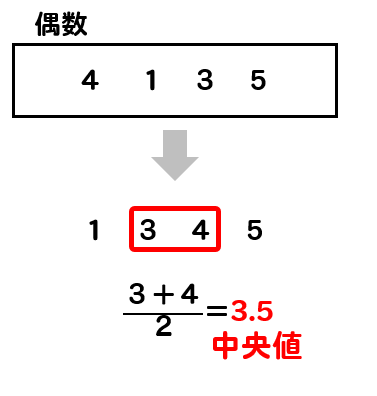
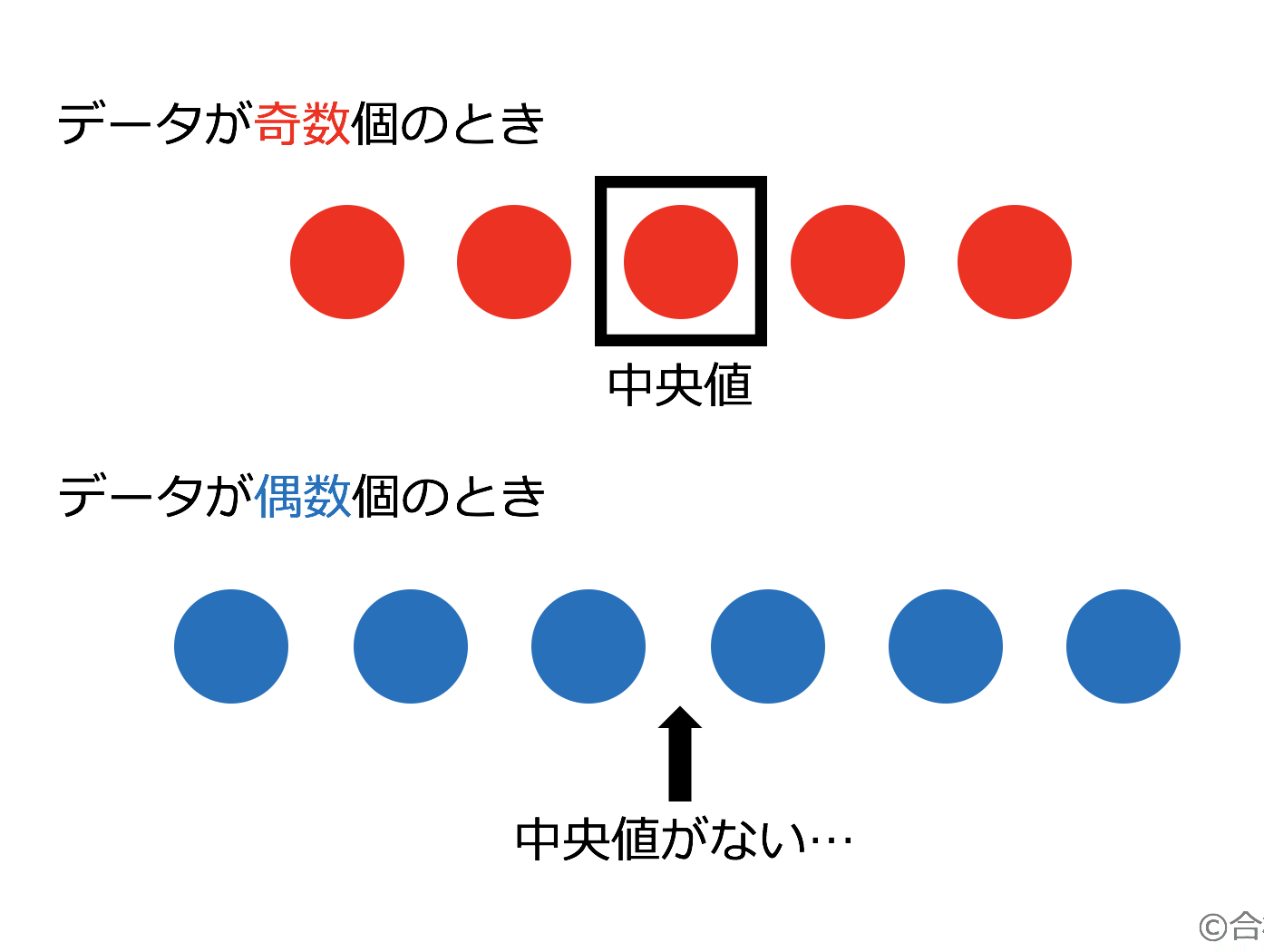
データが偶数の中央値の問題と求め方 クラスで仲の良い六人の数学のテストの成績が以下のようであるとき、中央値を求めなさい。 偶数の中央値の求め方 同じく、中央値が問われているので、まず与えられたデータを順番に並べます。 平均値/中央値の付近にデータが集積するような,左右対称・釣鐘型のデータの分布のこと です。実際には数学的に厳密な定義があるのですが,ここでは割愛します。 from wikipedia この様な場合であれば, 代表値として〈平均〉を用いても〈中央値〉を用いても,妥当な要約になる と言
中学 数学 中央値 問題
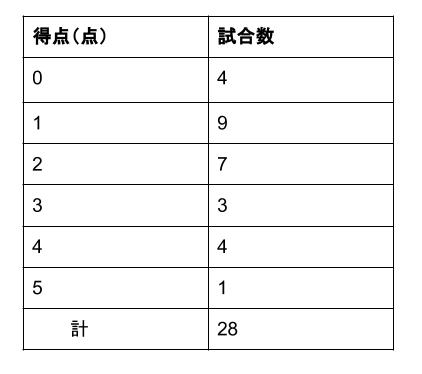
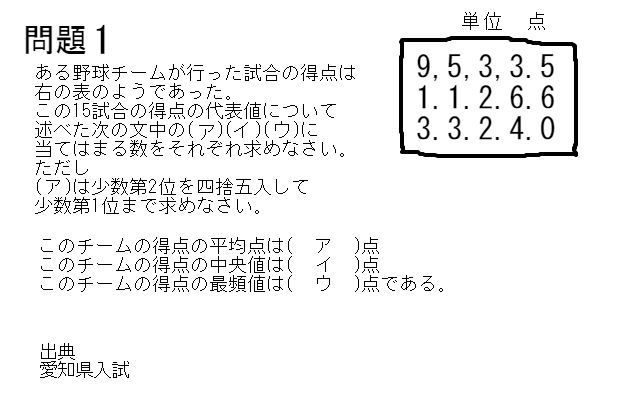
中学 数学 中央値 問題-代表値②(中央値を表・グラフから求める) 算数・数学塾フェルマータ 算数・数学塾フェルマータ ★山梨県の富士山麓にある算数・数学のオンライン学習塾です★ アウトドアや音楽、モノ作りなど色々なことが好きなパパ塾長(笑)が、数学を平均値、最頻値、中央値などがあります。このページでは、「最頻値」について学習しましょう。最頻値最頻値は、資料の中でもっとも多くあらわれる値のことで、モードともいいます。例1あるサッカーチームの \(1\) 試合の得点の記録このサッカーチームの \(1\) 試合の得点の最頻値は、\(1\) 点
データ分析小話 平均値と中央値の差について 数学 統計教室の和から株式会社
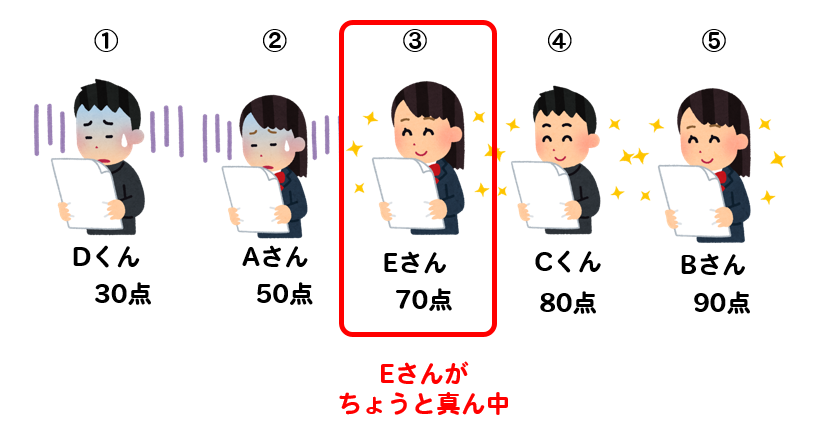
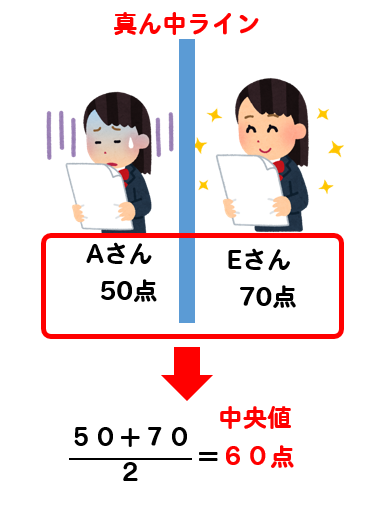
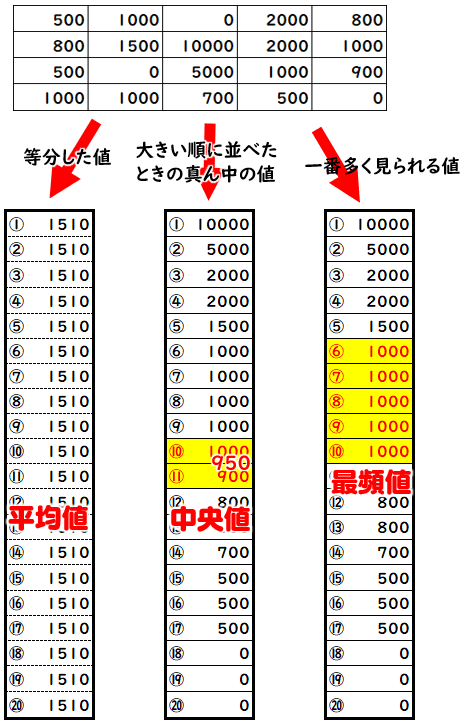
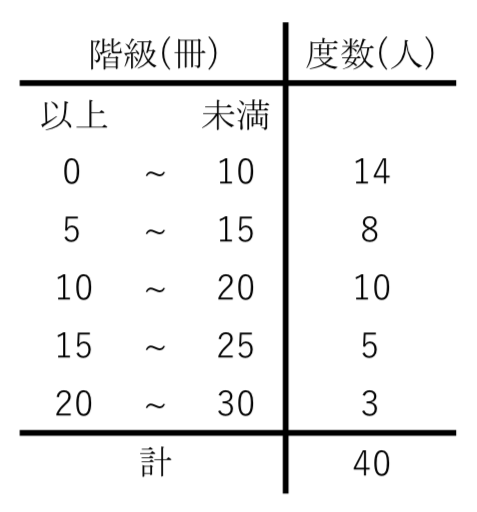
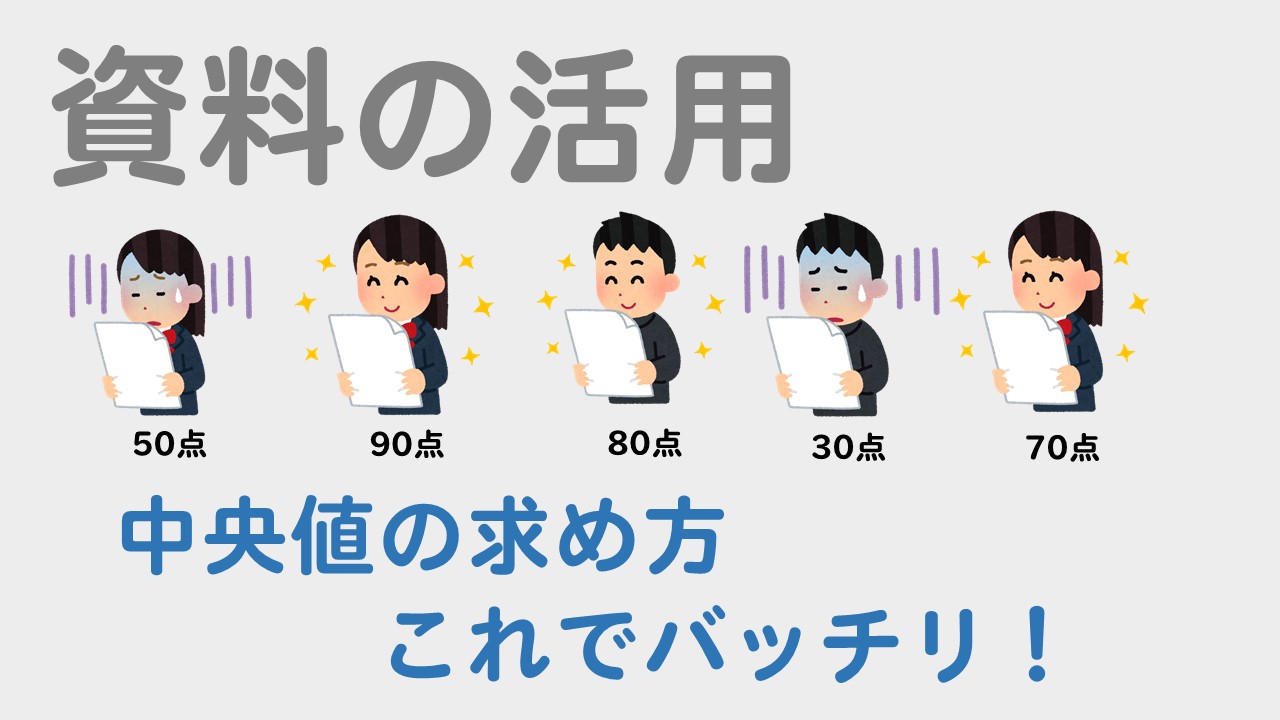
「平均値」 は、 「データの合計」 を 「全体の人数」 で 割った もの。 正に「平均」ってことだね。 「中央値」 は、 「中央」 、つまり 「真ん中の人の値」 のことだよ。 POINT 「平均値」の落とし穴! 体重の平均値の例で確認してみよう。 次のような、A君、B君、C君、D君、E君の5人の体重の平均値を考えよう。 平均値は? A君30kg B君40kg C君50kg D君60kg E君 170kg このとき「平均値」は017 中央値の求め方055 例題に挑戦(奇数バージョン)152 例題に挑戦(偶数バージョン)242 まとめ 中央値(メジアン)の求め方を3ステップで 特に、中央値(メジアン)や最頻値(モード)については数iibで初めて知ったという人も多く、馴染みのない言葉だと思います。 そこで、この記事では平均値・中央値・最頻値の3つについて、 求め方や計算方法などをそれぞれ解説していきたい と思います。
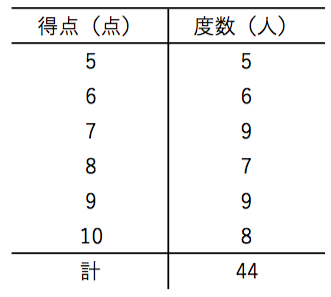
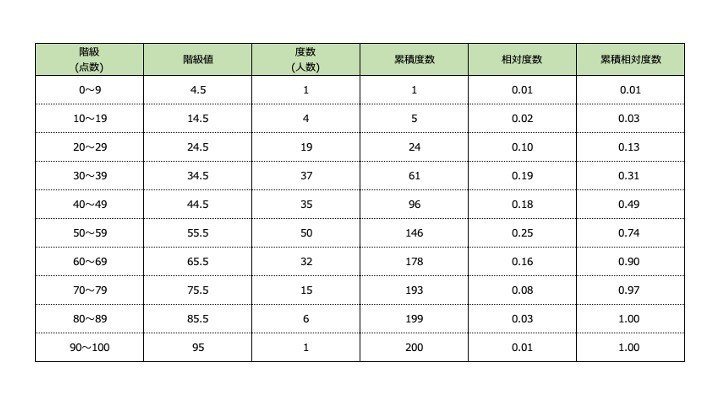
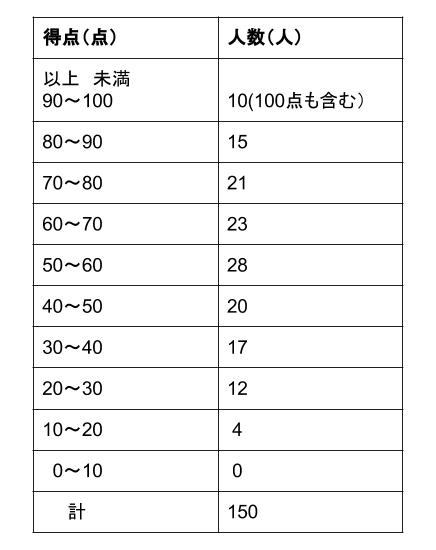
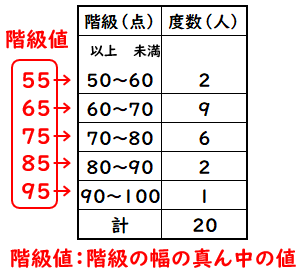
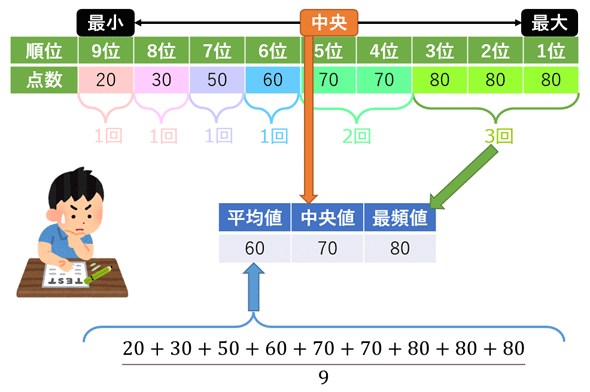
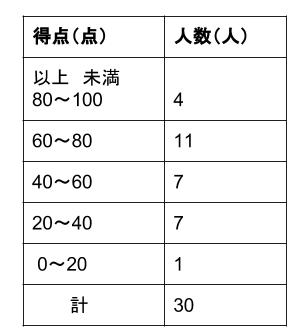
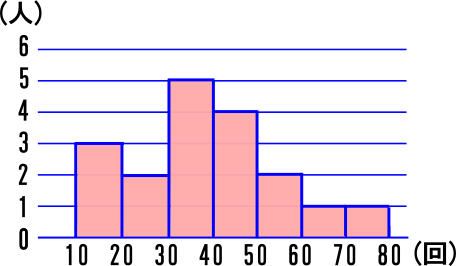
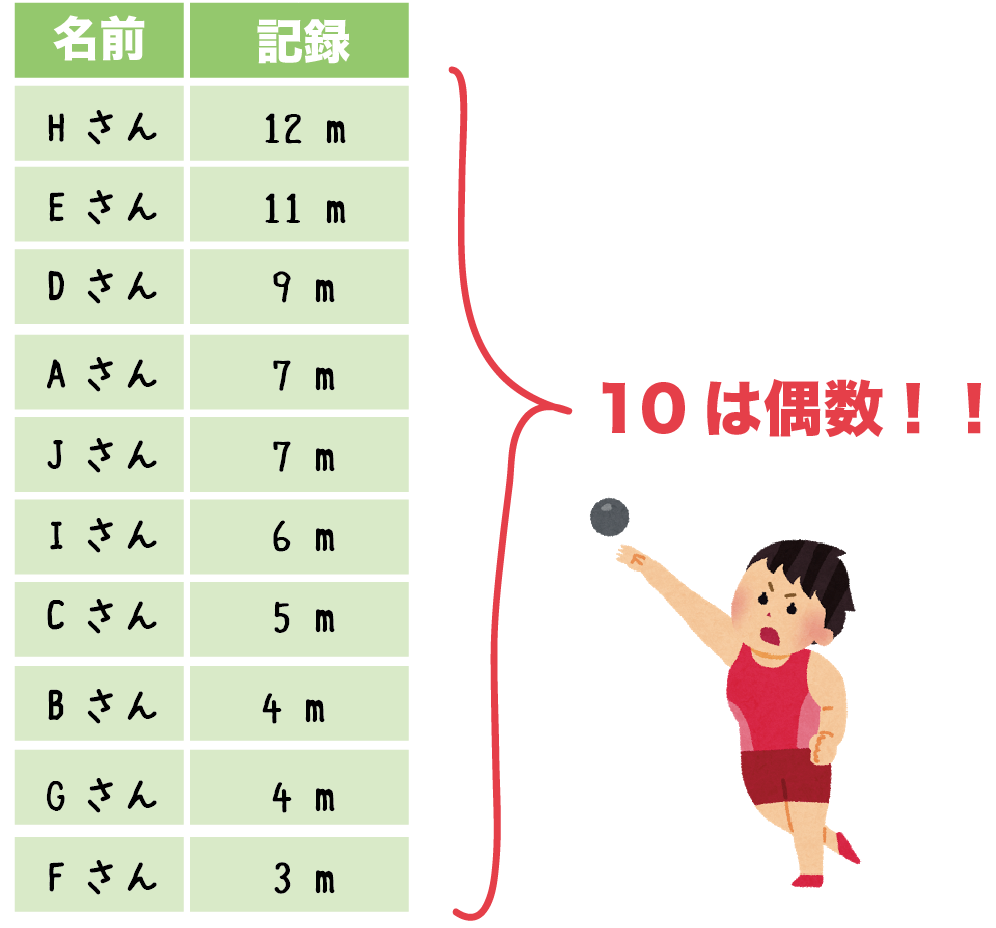
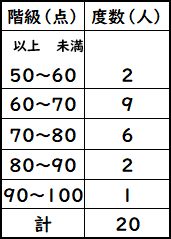
これについて、以下の問いに答えなさい。 1 男女それぞれの中央値(メジアン)を求めなさい。 ≪小さい順に並び替える≫ 男子 ⇒ 39、40、43、 44 、45、48、52 女子 ⇒ 35、37、38、 40 、 41 、42、43、45 ≪女子の中央値の計算≫ (40+41)÷2=40.5 ≪答≫ 男子の中央値:44kg、 女子の中央値: 40.5kg 2 男女それぞれの平均値を小数第二位まで求めなさい。 男子 ⇒ 階級値 ×度数の値を合計して、その値を度数の合計で割れば、平均値が出ます。 18/4/10 1−3の問題と解答の数値が一致していなかったので、プリントを入れかえました。 代表値 中央値 :資料の数値を小さい順に並べたときに中央に位置する値 メジアンと 中央値は、5番目と6番目の中央の値なので、 (2324)/2=235 (m) ・・・ (答) 2 (1) 度数合計が70なので、 ア=70 () =7062=8 ・・・ (答) (2) (170)/2=355 から、 中央値は、35番目と36番目の中央の値になる。 度数の累計から、 35番目と36番目が含まれる階級は、1 ~ 150 (答) 1分以上150分未満 3 Gの点数、Hの点数をG、Hとする。 条件から、 G>H ・
中学 数学 中央値 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「中学 数学 中央値 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 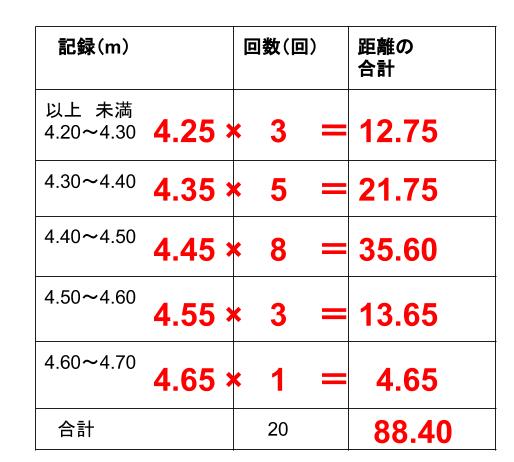 |
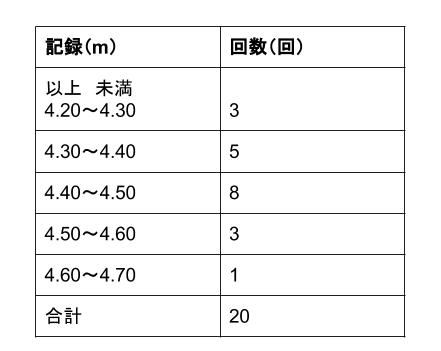
であり、真ん中の値は 159 159 と 156 156 です。 この 2 2 つの平均が、偶数個の資料の中央値です。 ()÷2 = 1575 ( 159 156) ÷ 2 = 1575 よって、求める中央値は 1575(cm) 1575 ( c m) です。 度数分布表からの中央値 度数分布表からは、各資料の真の値はわかりません。 よって、階級値を用います。 例1 表は、 A A さんの走り幅跳び 回の記録である。 中央値を求めなさい。 解説 togettercom 分布次第で「平均値」と「中央値」が乖離することがあるのは、義務教育でちゃんとやっていればわかるだろうに と思ったのですが、コメントの中に「義務教育でやってない時期がある」というものがありました。 教科書いまむかし 厳選とゆとりの時代(中学校) 大日本
Incoming Term: 中学 数学 中央値, 中学 数学 中央値 平均値, 中学 数学 中央値 求め方, 中学 数学 中央値 問題, 中学 数学 中央値とは, 中学 数学 資料の活用 中央値, 中学 数学 ヒストグラム 中央値, 中学 数学 度数分布表 中央値, 中学 数学 データ 中央値,




0 件のコメント:
コメントを投稿